FTorch
Facilitating Hybrid Modelling

Jack Atkinson

Senior Research Software Engineer
ICCS - University of Cambridge

2025-07-18

Precursors

Slides and Materials

To access links or follow on your own device these slides can be found at:
jackatkinson.net/slides

Licensing

Except where otherwise noted, these presentation materials are licensed under the Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0) License.

Vectors and icons by SVG Repo under CC0(1.0) or FontAwesome under SIL OFL 1.1

Motivation

Weather and Climate Models

Large, complex, many-part systems.

Parameteristion

Subgrid processes are largest source of uncertainty

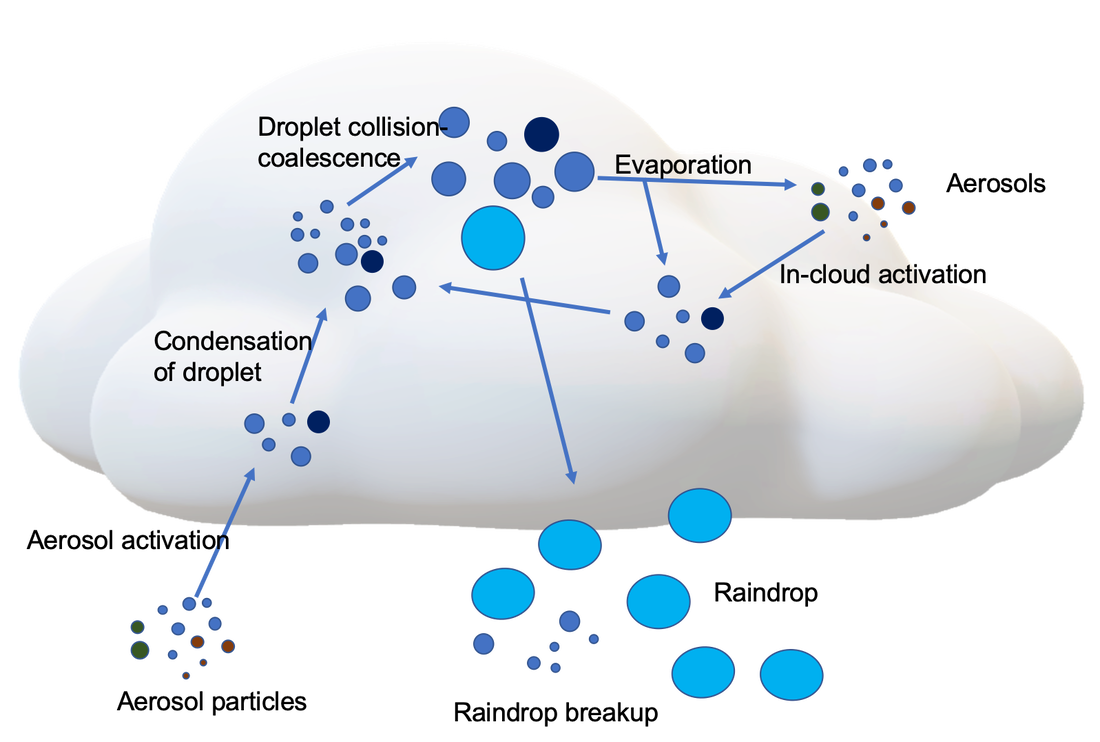
Microphysics by Sisi Chen Public Domain
Staggered grid by NOAA under Public Domain
Globe grid with box by Caltech under Fair use

Parameteristion

Subgrid processes are largest source of uncertainty

Microphysics by Sisi Chen Public Domain
Staggered grid by NOAA under Public Domain
Globe grid with box by Caltech under Fair use

Machine Learning in Science

We typically think of Deep Learning as an end-to-end process;
a black box with an input and an output¹.

Who’s that Pokémon?

\[\begin{bmatrix}\vdots\\a_{23}\\a_{24}\\a_{25}\\a_{26}\\a_{27}\\\vdots\\\end{bmatrix}=\begin{bmatrix}\vdots\\0\\0\\1\\0\\0\\\vdots\\\end{bmatrix}\] It’s Pikachu!

Neural Net by 3Blue1Brown under fair dealing.
Pikachu © The Pokemon Company, used under fair dealing.

1. And some models like GraphCast, FourCastNet, and Pangu operate on this principle

Hybrid Modelling

Neural Net by 3Blue1Brown under fair dealing.
Pikachu © The Pokemon Company, used under fair dealing.

2 approaches: * emulation, or * data-driven.

Additional challenges: * Physical compatibility * Physics-based models have conservation laws
Required for accuracy and stability * Language interoperation

Challenges

• Reproducibility
  • Ensure net functions the same in-situ
• Re-usability
  • Make ML parameterisations available to many models
  • Facilitate easy re-training/adaptation
• Language Interoperation

Language interoperation

Many large scientific models are written in Fortran (or C, or C++).
Much machine learning is conducted in Python.

Mathematical Bridge by cmglee used under CC BY-SA 3.0
PyTorch, the PyTorch logo and any related marks are trademarks of The Linux Foundation.”
TensorFlow, the TensorFlow logo and any related marks are trademarks of Google Inc.

Emulation and data-driven is a focus of several of our projects. CALIPSO, M2LInES, DataWave, etc.
Models typically in Fortran
ML typically in Python

Possible solutions

• Implement a NN in Fortran
  • Additional work, reproducibility issues, hard for complex architectures

• Forpy
  • Easy to add, harder to use with ML, GPL, barely-maintained

• SmartSim
  • Python ‘control centre’ around Redis: generic/versatile, learning curve, data copying

• Fortran-Keras Bridge
  • Keras only, abandonware(?)

Circa. 2022. More solutions emerging as the field grows e.g. TorchFort, Neural-Fortran, FIATS etc.

Efficiency

We consider 2 types:

Computational

Developer

In research both have an effect on ‘time-to-science’.
Especially when extensive research software support is unavailable.

1. No re-writing net after you have already done and trained
2. For scientists doing science, not compsci
3. Run on HPC environments so minimal additional
4. Easily keep up to date
5. Simple to learn and deploy
6. Needs to be as efficient as possible

FTorch

Approach

• PyTorch has a C++ backend and provides an API.
  
• Binding Fortran to C is straightforward¹ from 2003 using iso_c_binding.

We will:

• Save the PyTorch models in a portable Torchscript format
  • to be run by libtorch C++
• Provide a Fortran API
  • wrapping the libtorch C++ API
  • abstracting complex details from users

TorchScript is a statically typed subset of Python

1. A dangerous word, rather, ‘well supported’?

Approach

Python
env

Python
runtime

xkcd #1987 by Randall Munroe, used under CC BY-NC 2.5

Highlights - Developer

• Easy to clone and install
  • CMake, supported on linux/unix and Windows™

• Easy to link

  • Build using CMake,

  • or link via Make like NetCDF (instructions included)
    

    FCFLAGS += -I<path/to/install>/include/ftorch
    LDFLAGS += -L<path/to/install>/lib64 -lftorch

Find it on :

/Cambridge-ICCS/FTorch

Highlights - Developer

• User tools
  • pt2ts.py aids users in saving PyTorch models to Torchscript

• Examples suite
  • Take users through full process from trained net to Fortran inference

• Full API documentation online at
  cambridge-iccs.github.io/FTorch

• FOSS
  • licensed under MIT
  • contributions from users via GitHub welcome

Find it on :

/Cambridge-ICCS/FTorch

Highlights - Computation

• Use framework’s implementations directly
  • feature and future support, and reproducible

• Make use of the Torch backends for GPU offload
  • CUDA, HIP, MPS, and XPU enabled

• Indexing issues and associated reshape¹ avoided with Torch strided accessor.
• No-copy access in memory (on CPU).

Find it on :

/Cambridge-ICCS/FTorch

1. Or, the great row-major, column-major headache.

Highlights - Computation

• Indexing issues and associated reshape¹ avoided with Torch strided accessor.
• No-copy access in memory (on CPU).

Find it on :

/Cambridge-ICCS/FTorch

1. Or, the great row-major, column-major headache.

Some code

Model - Saving from Python

import torch
import torchvision

# Load pre-trained model and put in eval mode
model = torchvision.models.resnet18(weights="IMAGENET1K_V1")
model.eval()

# Create dummmy input
dummy_input = torch.ones(1, 3, 224, 224)

# Save to TorchScript
if trace:
    ts_model = torch.jit.trace(model, dummy_input)
elif script:
    ts_model = torch.jit.script(model)
frozen_model = torch.jit.freeze(ts_model)
frozen_model.save("/path/to/saved_model.pt")

TorchScript

• Statically typed subset of Python
• Read by the Torch C++ interface (or any Torch API)
• Produces intermediate representation/graph of NN, including weights and biases
• trace for simple models, script more generally

Fortran

 use ftorch
 
 implicit none
 
 real, dimension(5), target :: in_data, out_data  ! Fortran data structures
 
 type(torch_tensor), dimension(1) :: input_tensors, output_tensors  ! Set up Torch data structures
 type(torch_model) :: torch_net
 integer, dimension(1) :: tensor_layout = [1]
 
 in_data = ...  ! Prepare data in Fortran
 
 ! Create Torch input/output tensors from the Fortran arrays
 call torch_tensor_from_array(input_tensors(1), in_data, torch_kCPU)
 call torch_tensor_from_array(output_tensors(1), out_data, torch_kCPU)
 
 call torch_model_load(torch_net, 'path/to/saved/model.pt', torch_kCPU)  ! Load ML model
 call torch_model_forward(torch_net, input_tensors, output_tensors)      ! Infer
 
 call further_code(out_data)  ! Use output data in Fortran immediately
 
 ! Cleanup
call torch_delete(model)
call torch_delete(in_tensors)
call torch_delete(out_tensor)

GPU Acceleration

Cast Tensors to GPU in Fortran:

! Load in from Torchscript
call torch_model_load(torch_net, 'path/to/saved/model.pt', torch_kCUDA, device_index=0)

! Cast Fortran data to Tensors
call torch_tensor_from_array(in_tensor(1), in_data, torch_kCUDA, device_index=0)
call torch_tensor_from_array(out_tensor(1), out_data, torch_kCPU)

FTorch supports NVIDIA CUDA, ARM HIP, Intel XPU, and AppleSilicon MPS hardwares.

Use of multiple devices supported.

Effective HPC simulation requires MPI_Gather() for efficient data transfer.

Through developing a nice library it behaves as you would expect it to!
Familiar to pytorch users.
Pointer slinging is largely hidden from users.
Data transposition is taken care of by us (but options available for users to handle).

Publication & tutorials

FTorch is published in JOSS!

Atkinson et al. (2025)
FTorch: a library for coupling PyTorch models to Fortran.
Journal of Open Source Software, 10(107), 7602,
doi.org/10.21105/joss.07602

Please cite if you use FTorch!

In addition to the comprehensive examples in the FTorch repository we provide an online workshop at /Cambridge-ICCS/FTorch-workshop

Applications and Case Studies

MiMA - proof of concept

• The origins of FTorch
  • Emulation of existing parameterisation
  • Coupled to an atmospheric model using forpy in Espinosa et al. (2022)¹
  • Prohibitively slow and hard to implement
  • Asked for a faster, user-friendly implementation that can be used in future studies.

• Follow up paper using FTorch: Uncertainty Quantification of a Machine Learning Subgrid-Scale Parameterization for Atmospheric Gravity Waves (Mansfield and Sheshadri 2024)
  • “Identical” offline networks have very different behaviours when deployed online.

Model of an idealised Moist Atmosphere online at /DataWaveProject/MiMA-machine-learning

1. Originally written in TensorFlow…

ICON

• Icosahedral Nonhydrostatic Weather and Climate Model
  • Developed by DKRZ (Deutsches Klimarechenzentrum)
  • Used by the DWD and Meteo-Swiss

• Interpretable multiscale Machine Learning-Based Parameterizations of Convection for ICON (Heuer et al. 2023)¹
  • Train U-Net convection scheme on high-res simulation
  • Deploy in ICON via FTorch coupling
  • Evaluate physical realism (causality) using SHAP values
  • Online stability improved when non-causal relations are eliminated from the net

Running on JUWELS at the Jülich Supercomputing Centre; ICON Model is now available at gitlab.dkrz.de/icon/icon-model

1. Work without direct involvement of ICCS - success on ‘ease of use’ of FTorch

CESM coupling

• The Community Earth System Model
• Part of CMIP (Coupled Model Intercomparison Project)
• Make it easy for users
  • FTorch integrated into the build system (CIME)
    • /Cambridge-ICCS/cime_je
  • libtorch is included on the software stack on Derecho
    • Improves reproducibility

Derecho by NCAR

Work done with Will Chapman and Jim Edwards of NCAR.
CIME with FTorch is available with instructions /Cambridge-ICCS/cime_je

Others

• To replace a BiCGStab bottleneck in the GloSea6 Seasonal Forecasting model
  (Park and Chung 2025).
• Bias correction of CESM through learning model biases compared to ERA5
  (Chapman and Berner 2025)
• Implementation of nonlinear interactions in the WaveWatch III model
  (Ikuyajolu et al. 2025).
• Stable embedding of a convection resolving parameterisation in E3SM
  (Hu et al. 2025).
• Implementation of a new convection trigger in the CAM model.
  Miller et al. In Preparation.
• Embedding of ML schemes for gravity waves in the CAM model.
  ICCS & DataWave.

Online Training and AutogradWork

Work led by Joe Wallwork

What and Why?

To date FTorch has focussed on enabling researchers to run models developed and trained offline within Fortran codes.

However, it is clear (Mansfield and Sheshadri 2024) that more attention to online performance, and options with differentiable/hybrid models (e.g. Kochkov et al. 2024) is becoming important.

Pros:

• Avoids saving large volumes of training data.
• Avoids need to convert between Python and Fortran data formats.
• Possibility to expand loss function scope to include downstream model code.

Cons:

• Difficult to implement in most frameworks.

Expanded Loss function

Suppose we want to use a loss function involving downstream model code, e.g.,

\[J(\theta)=\int_\Omega(u-u_{ML}(\theta))^2\;\mathrm{d}x,\]

where \(u\) is the solution from the physical model and \(u_{ML}(\theta)\) is the solution from a hybrid model with some ML parameters \(\theta\).

Computing \(\mathrm{d}J/\mathrm{d}\theta\) requires differentiating Fortran code as well as ML code.

Implementing AD in FTorch

• Expose autograd functionality from Torch.
  • e.g., requires_grad argument and backward methods.
• Overload mathematical operators (=,+,-,*,/,**).

Using AD - FTorch

use ftorch

type(torch_tensor) :: a, b, Q, multiplier, divisor, dQda, dQdb
real, dimension(2), target :: Q_arr, dQda_arr, dQdb_arr

! Construct input tensors with requires_grad=.true.
call torch_tensor_from_array(a, [2.0, 3.0], torch_kCPU, requires_grad=.true.)
call torch_tensor_from_array(b, [6.0, 4.0], torch_kCPU, requires_grad=.true.)

! Workaround for scalar multiplication and division using 0D tensors
call torch_tensor_from_array(multiplier, [3.0], torch_kCPU)
call torch_tensor_from_array(divisor, [3.0], torch_kCPU)

! Compute some mathematical expression
call torch_tensor_from_array(Q, Q_arr, torch_kCPU)
Q = multiplier * (a**3 - b * b / divisor)

! Reverse mode
call torch_tensor_backward(Q)
call torch_tensor_from_array(dQda, dQda_arr, torch_kCPU)
call torch_tensor_from_array(dQdb, dQdb_arr, torch_kCPU)
call torch_tensor_get_gradient(a, dQda)
call torch_tensor_get_gradient(b, dQdb)
print *, dQda_arr
print *, dQdb_arr

Optimizers and loss functions

• Optimizers
  • Expose torch::optim::SGD, torch::optim::AdamW etc., as well as zero_grad and step methods.
  • This already enables some cool AD applications in FTorch.
• Loss functions
  • We haven’t exposed any built-in loss functions yet.
  • Implemented torch_tensor_sum and torch_tensor_mean, though.

Putting it together - running an optimiser in FTorch

\[\begin{bmatrix}f_1\\f_2\\f_3\\f_4\end{bmatrix}=\mathbf{f}(\mathbf{x};\mathbf{a})=\mathbf{a}\bullet\mathbf{x}\equiv\begin{bmatrix}a_1x_1\\a_2x_2\\a_3x_3\\a_4x_4\end{bmatrix}\] Starting from \(\mathbf{a}=\mathbf{x}:=\begin{bmatrix}1,1,1,1\end{bmatrix}^T\), optimise the \(\mathbf{a}\) vector such that \(\mathbf{f}(\mathbf{x};\mathbf{a})=\mathbf{b}:=\begin{bmatrix}1,2,3,4\end{bmatrix}^T\).

Loss function: \(\ell(\mathbf{a})=\overline{(\mathbf{f}(\mathbf{x};\mathbf{a})-\mathbf{b})^2}\).

Putting it together - running an optimiser in FTorch

In both cases we achieve \(\mathbf{f}(\mathbf{x};\mathbf{a})=\begin{bmatrix}1,2,3,4\end{bmatrix}^T\).

Case study - UKCA

• Implicit timestepping, quasi-Newton, full LU decomposition.
• For each time subinterval to be integrated:
  • Start with \(\Delta t=3600\).
  • Try to integrate with the current timestep size.
  • If any grid-box fails, half the step and try again.
• A nice ‘safe’ application of machine learning in modelling

Summary

• Use of ML within traditional numerical models
  • A growing area that presents challenges
• Language interoperation
  • FTorch provides a solution for scientists looking to implement torch models in Fortran
  • Designed with both computational and developer efficiency in mind
  • Has helped deliver science in climate research and beyond
    (Heuer et al. (2023), Mansfield and Sheshadri (2024))
  • Built into CESM to allow the userbase access
• FTorch is exploring options for online training and AD
  • Torch autograd functionality exposed using iso_c_binding.
  • Exposed tools for optimization.
  • Work in progress on setting up online ML training.

Thanks for Listening

Get in touch:

 Jack Atkinson

 jackatkinson.net

 jwa34[AT]cam.ac.uk

 jatkinson1000

 @jatkinson1000@hachyderm.io

Find it on :

/Cambridge-ICCS/FTorch

Thanks to Joe Wallwork, Tom Metlzer, Elliott Kasoar
and the rest of the FTorch team.

FTorch has been supported by

The ICCS received support from

References

Atkinson, Jack, Athena Elafrou, Elliott Kasoar, Joseph G. Wallwork, Thomas Meltzer, Simon Clifford, Dominic Orchard, and Chris Edsall. 2025. “FTorch: A Library for Coupling PyTorch Models to Fortran.” Journal of Open Source Software 10 (107): 7602. https://doi.org/10.21105/joss.07602.

Chapman, William E, and Judith Berner. 2025. “Improving Climate Bias and Variability via CNN-Based State-Dependent Model-Error Corrections.” Geophysical Research Letters 52 (6): e2024GL114106. https://doi.org/10.1029/2024GL114106.

Espinosa, Zachary I, Aditi Sheshadri, Gerald R Cain, Edwin P Gerber, and Kevin J DallaSanta. 2022. “Machine Learning Gravity Wave Parameterization Generalizes to Capture the QBO and Response to Increased CO2.” Geophysical Research Letters 49 (8): e2022GL098174.

Heuer, Helge, Mierk Schwabe, Pierre Gentine, Marco A Giorgetta, and Veronika Eyring. 2023. “Interpretable Multiscale Machine Learning-Based Parameterizations of Convection for ICON.” arXiv Preprint arXiv:2311.03251.

Hu, Zeyuan, Akshay Subramaniam, Zhiming Kuang, Jerry Lin, Sungduk Yu, Walter M Hannah, Noah D Brenowitz, Josh Romero, and Michael S Pritchard. 2025. “Stable Machine-Learning Parameterization of Subgrid Processes in a Comprehensive Atmospheric Model Learned from Embedded Convection-Permitting Simulations.” Journal of Advances in Modeling Earth Systems 17 (7): e2024MS004618.

Ikuyajolu, Olawale James, Luke P Van Roekel, Steven R Brus, and Erin E Thomas. 2025. “NLML: A Deep Neural Network Emulator for the Exact Nonlinear Interactions in a Wind Wave Model.” Authorea Preprints. https://doi.org/10.22541/essoar.174366388.80605654/v1.

Kochkov, Dmitrii, Janni Yuval, Ian Langmore, Peter Norgaard, Jamie Smith, Griffin Mooers, Milan Klöwer, et al. 2024. “Neural General Circulation Models for Weather and Climate.” Nature 632 (8027): 1060–66. https://doi.org/10.1038/s41586-024-07744-y.

Mansfield, Laura A, and Aditi Sheshadri. 2024. “Uncertainty Quantification of a Machine Learning Subgrid-Scale Parameterization for Atmospheric Gravity Waves.” Authorea Preprints.

Park, Hyesung, and Sungwook Chung. 2025. “Utilization of a Lightweight 3D u-Net Model for Reducing Execution Time of Numerical Weather Prediction Models.” Atmosphere 16 (1): 60.